Branch-SCvx (Branched Trajectory Optimization)

Branched Trajectory Optimization establishes a unique, general purpose method for establishing graphs of trajectory optimization problems, and leads to a tractable formulation for contingency planning in the presence of unknown multimodal uncertainty distributions. This work is soon to be submitted to the Transactions on Robotics (T-RO) journal. The problem is formulated in continuous time, and then solved with the continuous-time successive convexification (CT-SCvx) framework with continuous-time constraint satisfaction guarantees, leading to the Branch Successive Convexification (Branch-SCvx) formulation.

 

 

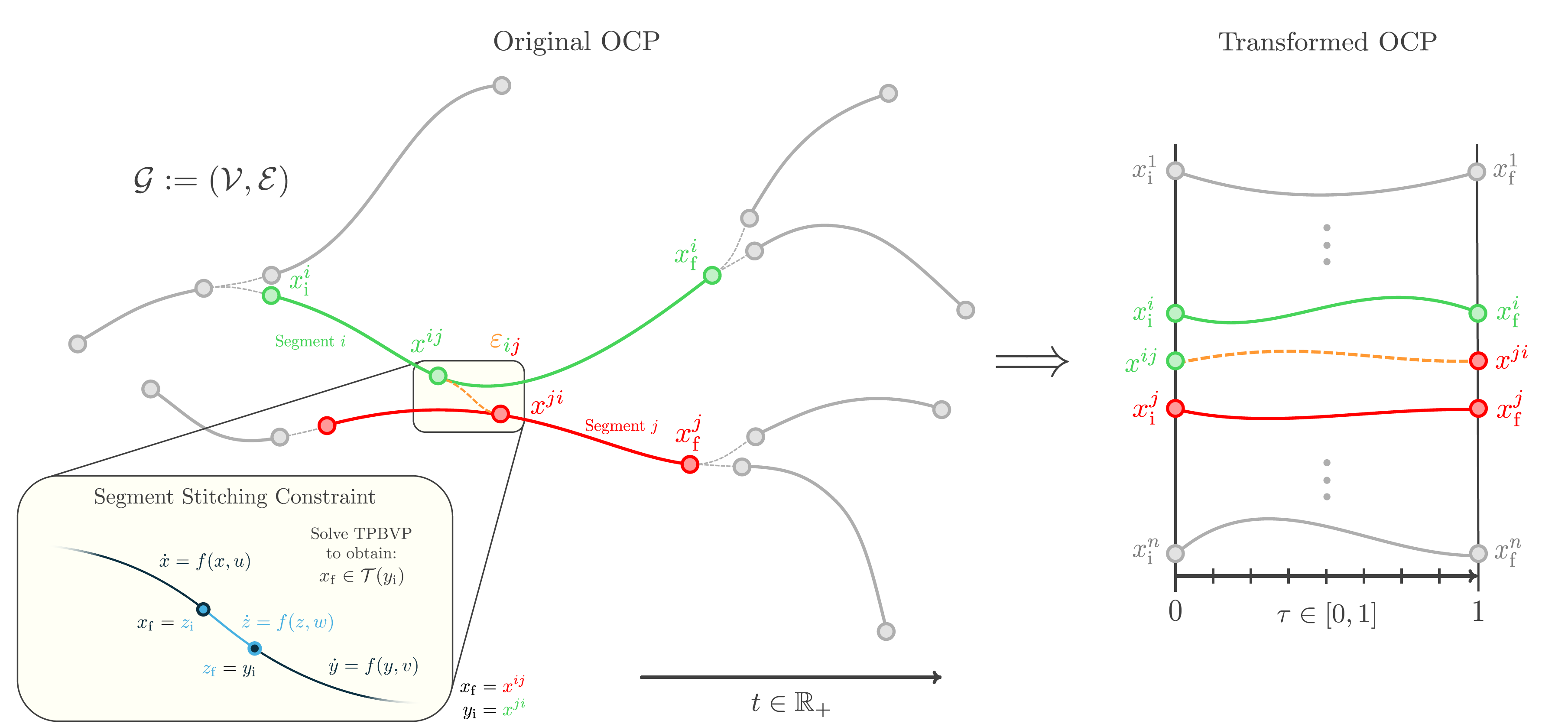
The model begins with instantiation of a graph, where vertices represent trajectory segments, and edges represent connections between segments, with additional structure to make these connections physically realizable and numerically efficient during transcription. Consequently, it can be shown that the Deferred Decision Trajectory Optimization (DDTO) problem model can be obtained through additional structure (notably, through restriction of the trajectory graph to be an arboresence), which supports the aforementioned contingency planning operations through modeling of multiple targets with an objective to defer decision to commit to any given target for as long as possible (thus keeping all targets reachable for as long as possible).

This work has been successfully applied to the HALO project (which is discussed more on this page), with additional nonconvex constraints which were unable to be modeled previously, including: (1) a nonlinear drag term in the dynamics, (2) explicit free-final-time modeling and (3) cylindrical obstacle avoidance constraints.

 

 

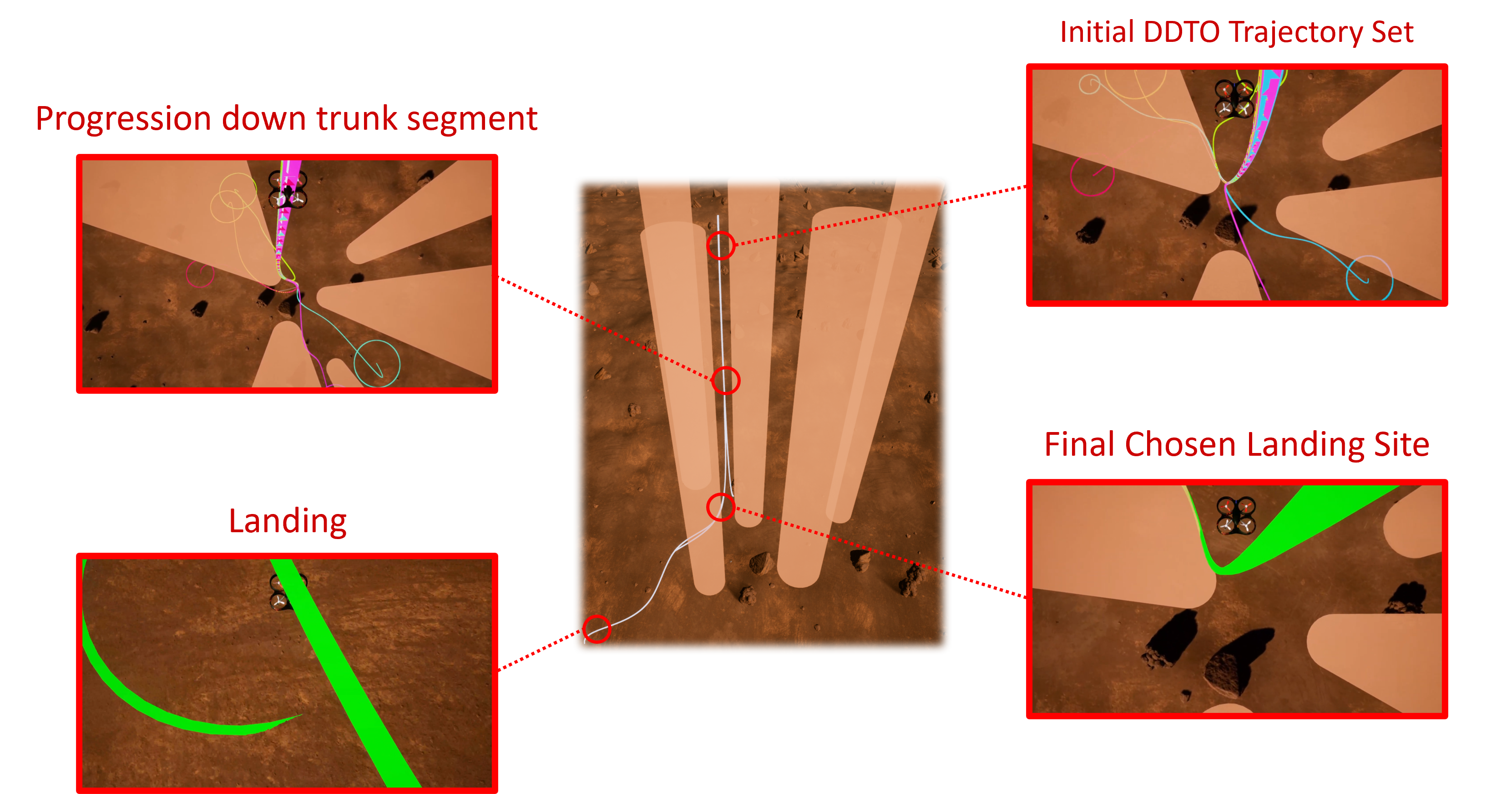
I have also developed a custom GUI implementation of Branch-SCvx applied to the DDTO problem (building on the GUI work in this paper) and performed hardware experiments with the ACL lab’s inhouse quadrotors in a netted cage environment.